Free Boundary Problem Modeling Arterial Plaque
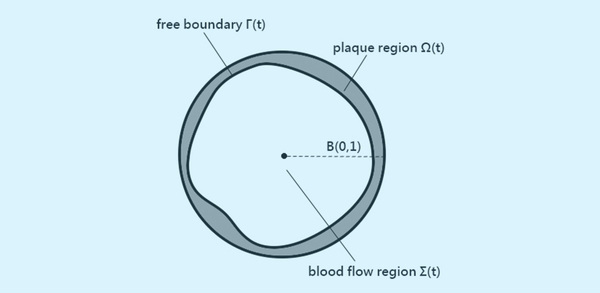
Atherosclerosis, hardening of the arteries, originates from small plaque in the arteries; it is a major cause of disability and premature death in the United States and worldwide. In this project, we study the bifurcation for a highly nonlinear and highly coupled PDE model describing the growth of arterial plaque. The model involves LDL and HDL cholesterols, macrophage cells as well as foam cells, with the interface separating the plaque and blood flow region being a free boundary. We establish a finite branch of symmetry-breaking stationary solutions which bifurcate from the radially symmetric solutions. Since plaque in reality is unlikely to be strictly radially symmetric, our result would be useful to explain the asymmetric shapes of plaque.
(Bei Hu)